J.Gong
2025-09-09
3.08min
Using Mini-Max Algorithm to Play Tetris 🎮
So here’s a funny story - when my teacher first mentioned the “Mini-Max Algorithm,” I immediately thought of that AI company 😅. Had no clue it was actually a classic game theory algorithm!
But then he showed us this simple example: two players take turns moving the same piece either 1 or 2 steps forward. First one to reach the end wins. That’s when it clicked! 💡
You basically build a binary tree and find leaves that equal 0 or less. Count the branches - if it’s odd, player wins; if even, PC wins. Pretty neat, right?
This is actually super close to the real Mini-Max algorithm! The core idea is simple: calculate the worst-case scenario for your opponent while maximizing your own benefit.
Let’s think about it this way - at my turn, which move gives me the best advantage? 🤔
Let’s define our win conditions:
Mini-Max Decision Tree Structure 🌳
Here’s how the decision tree should look:
graph LR
Root(("Root"))
Root --> L(("Player 1"))
Root --> R(("Player 2"))
L --> LL(("AI 1"))
L --> LR(("AI 2"))
R --> RL(("AI 1"))
R --> RR(("AI 2"))
LL --> LLL(("..."))
LR --> LRL(("..."))
RL --> RLL(("..."))
RR --> RLR(("..."))
LLL --> LLLL(("1"))
LRL --> LRLL(("-1"))
RLL --> RLLL(("-1"))
RLR --> RLRL(("1"))
Every time the AI moves, it calculates all possible outcomes. For example: if Player1 → AI1 leads to +1 but Player1 → AI2 leads to -1, then max("Player1 → AI1", "Player1 → AI2") is obviously Player1 → AI1. So the AI should take 1 step.
The cool part? The AI can also predict player moves and choose the branch where even if the player gets minimum benefit, the AI can still win! 🧠
Building a 1v1 Tetris Game 🎯
Now here’s where it gets interesting - let’s create a competitive Tetris game: Player VS AI!
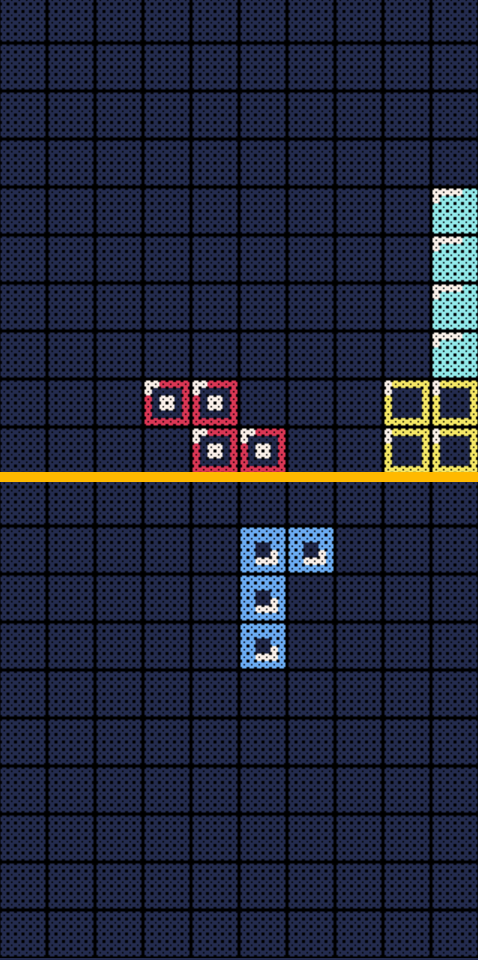
Game Start: Player and AI split the screen - you’re on the bottom playing regular Tetris, AI gets the top half 🎮
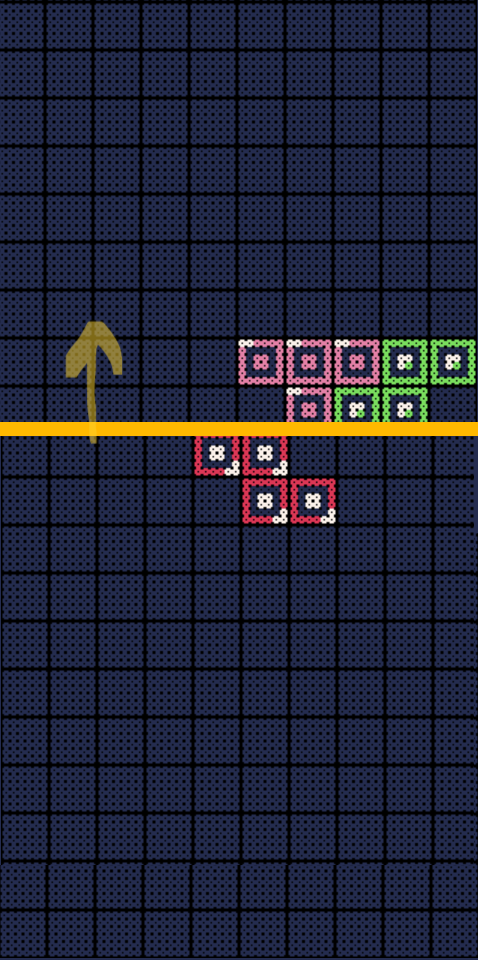
The Twist: When either side clears a row, they get rewarded with +1 row of space, while their opponent loses one row! Talk about pressure! 😤
The game continues until someone runs out of space to place pieces. It’s like Tetris meets territorial warfare! ⚔️
Scoring System - The Math Behind the Magic 🧮
To make Mini-Max work, we need a solid scoring system. Let me break down how we evaluate each possible move:

Tetris Board Evaluation Example: Here’s what happens when we drop this “Z” piece without rotation
Let’s look at our key metrics:
🏗️ Height:
Lower is better - we don’t want towering stacks!
🧹 Cleared Rows:
Higher is better - more cleared rows = more points
🕳️ Holes:
Lower is better - holes are the enemy of Tetris
📈 Gradient:
Lower is better - we want smooth, even surfaces
Finding the Perfect Coefficients 🎯
Now we need to weight these factors. Our scoring formula looks like this:
Instead of reinventing the wheel, I found that someone already solved this using Genetic Algorithms 🧬. Here are the magic numbers:
Implementing Mini-Max in Tetris, First Try 🤖
Here’s where it gets tricky - Tetris pieces are random! So our decision tree height is usually just 1. But if we know the next few pieces in the sequence, we can go deeper.
Move Analysis for Each Piece:
| Horizontal Movement (9 positions) 🔄 | Rotation Options (4 rotations) 🌀 |
|---|---|
 |  |
For each piece, we typically have around 36 possible moves (9 positions × 4 rotations). Consider if we show a sequence of pieces not only one, the calculation will be . Definately need pruning.
Another thing… this game currently only uses the Max part of the Mini-Max algorithm 🤯.
Yeah… I think I need to change my plan.
🎮 Change into Turns Game
Ohh, wait! I might have overcomplicated things 😅.
What if I make it a turn-based game? The player and the AI take turns.
Each turn, I’ll show two pieces:
- one for the current player,
- one for the opponent.
That way, the AI can actually use the full Mini-Max algorithm! 🧠✨
📜 Rules
So, what about the rules… 🤔
Classic Tetris scoring looks like this:
| Row clear | Points |
|---|---|
| Single | 100 |
| Double | 300 |
| Triple | 500 |
| Tetris | 800 |
There are also some high-level moves like T-Spin (when you rotate the T piece at the very last moment to clear rows).
I probably won’t implement it (too tricky to test 😅), but here are the points anyway:
| Row clear | Points |
|---|---|
| Single | 800 |
| Double | 1200 |
| Triple | 1600 |
And don’t forget Combos 🔥 — every time you chain clears, you get +50 points extra.
👉 Wanna try it out? Play the game here: pixtris.vercel.app 🎉
unfinished